Самопроверка

1.     Установите, можно ли преобразовать уравнение к виду линейной функции

 у = kx+m? Если да, то укажите коэффициенты этой линейной функции и постройте график.

Решение.

а) 3 = - 6у. Это уравнение не является линейным уравнением с двумя переменными х и у. Но его можно представить в виде линейного уравнения с двумя переменными х и у.

6у + 0х +3 = 0

Это уравнение можно преобразовать к виду линейной функции у = kx + m.

У = 0х – 0,5;  k = 0 ;    m = - 0,5.

У = - 0,5. Это есть прямая, пересекающая ось ординат в точке – 0,5 и параллельна оси абсцисс. Построим график.

б) Уравнение  2х – у = 4 является линейным уравнением с двумя переменными. Его можно преобразовать к виду линейной функции у = kx + m. Для этого выразим у через х:    

- у = - 2х + 4;

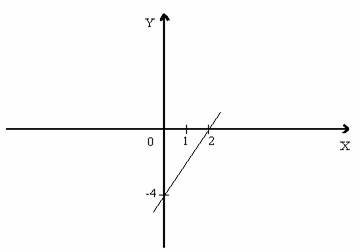
   у = 2х – 4,  то есть к виду у = kx = m. Тогда  k = 2;  m = - 4. Построим график. Графиком является прямая линия..  Для ее построения достаточно построить две точки, принадлежащие этому графику. Составим таблицу для двух значений.

НАЗАД