ТЕМА: «Линейная функция».
ПРАКТИКУМ
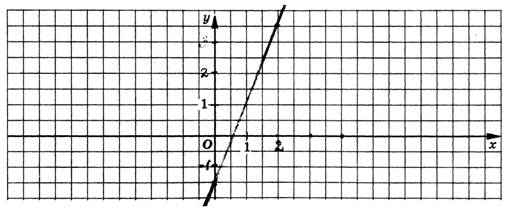
Задание 1. Установите, можно ли преобразовать уравнение к виду линейной функции у = kx + m, и если да, то укажите коэффициенты этой линейной функции и постройте ее график.
а) 3 = 5х – 2у
РЕШЕНИЕ:
Данное уравнение является линейным уравнением с двумя переменными х и у. Его можно преобразовать к виду линейной функции у = kx+m.
2у = 5х + (-3);
у = 2,5х + (-1,5).
Здесь k = 2,5 ; m = -1,5
Графиком линейной функции является прямая линия. Чтобы ее построить, достаточно найти значения функции в двух точках, например, в точках х=0 и х=2.
|
х |
0 |
2 |
|
у |
-1,5 |
3,5 |
Построим искомый график.

![]() б)
3 = 2х
б)
3 = 2х
Уравнение 3 = 2х не является линейным уравнением с двумя переменными х и у. Его можно записать в виде линейного уравнения: 2х + 0у – 3 = 0, но нельзя преобразовать к виду линейной функции у = kx+m, так как на ноль делить нельзя.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.
Установите, можно ли преобразовать уравнение к виду линейной функции y = kx+m? Если да, то укажите коэффициенты этой линейной функции и постройте ее график:
а) 3 = - 6 у;
б) 2х - у = 4.
Задание 2. Постройте график линейной функции у = 2х – 5 и найдите для нее наибольшее и наименьшее значения функции на отрезке [1; 4]
Решение.
Графиком линейной функции является прямая линия. Нужно построить прямую линию, затем выделить промежуток этой прямой, концами которого являются точки, абсциссы которых равны 1 и 4.
Если конец промежутка принадлежит графику, он выделяется темным кружком. В данном случае оба конца принадлежат графику.
Составим таблицу для двух значений функции:
|
Х |
2 |
3 |
|
у |
-1 |
1 |
Построим график функции.
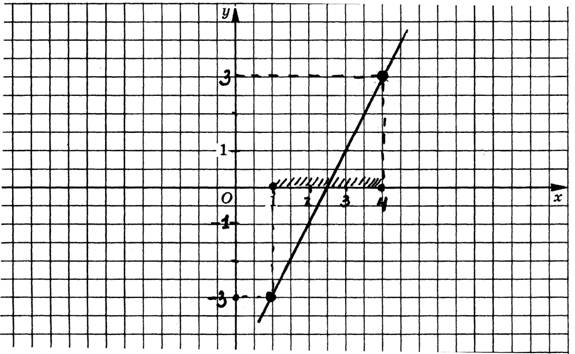
Найдем наибольшее и наименьшее значения функции на заданном промежутке.
Ответ: наибольшее значение функции равно 3 при х = 4; наименьшее значение функции равно -3 при х = 1
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.
Постройте график линейной функции у = 3х + 1 и найдите для нее наибольшее и наименьшее значения функции на отрезке [1; 2] .
Задание 3. Установите, задает ли прямую пропорциональность уравнение, и, если задает, то укажите коэффициент пропорциональности:
а) х = 2у;
б) х = 2/у;
в) –х = у/2.
Решение:
а) х = 2у. Выразим у через х. Получим: у = х/2.
Уравнение задает прямую пропорциональность у = kx. Коэффициент пропорциональности k = ½.
б) х = 2/у. Выразим у через х. Получим: у = 2/х. Уравнение не задает прямую пропорциональность у = kx.
в) –х = у/2. Выразим у через х. Получим: у = -2х. Уравнение задает прямую пропорциональность вида у = kx . Коэффициент пропорциональности k = -2.
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.
Установите, задает ли прямую пропорциональность уравнение, и, если задает, то укажите коэффициент пропорциональности: а) х/у = 2; б) у/х = 2
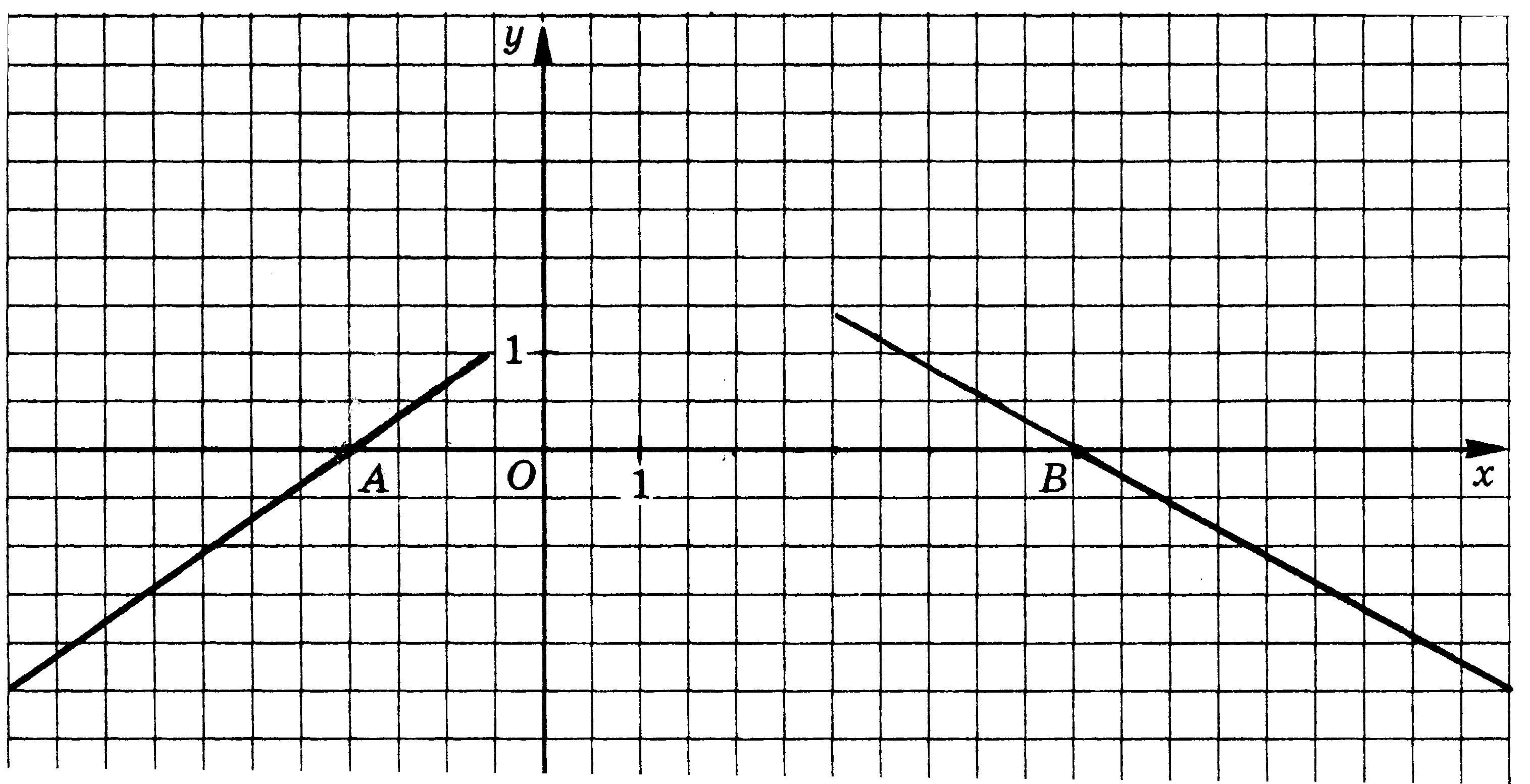
Задание 4.На рисунке представлены графики двух линейных функций. Установите:
1) при каком значении х будет у = 0;
2) при каких значениях х будет у<0;
3) при каких значениях х будет у>0;
4) какой знак имеет угловой коэффициент для каждой из этих линейных функций;
5) какая из линейных функций возрастает, какая – убывает?
Решение
1)У линейной функции, график которой проходит через точку А, у = 0 при х = -2; у линейной функции, график которой проходит через точку В, у = 0 при х = 5,5.
2) У линейной функции, график которой проходит через точку А, у<0 при х<-2; у линейной функции, график которой проходит через точку В, у<0 при х>5,5.
3)У линейной функции, график которой проходит через точку А, у>0 при х>-2, у линейной функции, график которой проходит через точку В, у>0 при х<5,5.
4)У линейной функции, график которой проходит через точку А, угловой коэффициент положительный, так как график образует с положительным направлением оси абсцисс острый угол.
У линейной функции, график которой проходит через точку В, угловой коэффициент отрицательный, так как образует с положительным направлением оси абсцисс тупой угол.
5) Линейная функция, график которой проходит через точку А, возрастает, так как если двигаться по этому графику слева направо, то ординаты точек увеличиваются. Значит, большему значению аргумента соответствует большее значение функции (возрастающая функция).
Линейная функция, график которой проходит через точку В, убывает, так как если двигаться по графику слева направо, то ординаты точек уменьшаются. Значит, большему значению аргумента соответствует меньшее значение функции (убывающая функция).
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
На рисунке представлен график линейной функции. Установите:
1) при каком значении х будет у = 0;
2) при каких значениях х будет у<0;
3) при каких значениях х будет у>0;
4) какой знак имеет угловой коэффициент этой прямой?
5) Это возрастающая или убывающая функция?

Задание 5. Найдите (не строя график) координаты точки графика линейной функции у = 2х – 4, абсцисса которой равна ее ординате.
Решение
По условию, х = у. Поэтому в уравнение, которым задана линейная функция, вместо у можно подставить х, или вместо х подставить у. Получаем уравнение х = 2х – 4 или у = 2у – 4. Решив одно из этих уравнений, получим х = у = 4.
Ответ: ( 4 ;4 )
Задание 6. Установите, не строя графики, параллельны или пересекаются прямые. Если прямые пересекаются, то найдите координаты точки пересечения.
1) у = 2х – 1 и у = 2х + 1
2) у = 3х – 1 и у = -3х + 1
Решение
Графики линейных функций параллельны, если равны их угловые коэффициенты. Если же угловые коэффициенты не равны, то графики линейных функций имеют одну общую точку (пересекаются).
1)у = 2х – 1 и у = 2х + 1.Угловой коэффициент функции у = 2х – 1 равен 2. Угловой коэффициент прямой у = 2х + 1 тоже равен 2, следовательно, угловые коэффициенты этих прямых равны, а значит, прямые параллельны.
2)у = 3х – 1. Угловой коэффициент этой прямой равен 3.
У = - 3х + 1. Угловой коэффициент этой прямой равен – 3. Следовательно угловые коэффициенты этих прямых не равны, а значит, прямые не параллельны (имеют одну общую точку, точку пересечения). У точки пересечения рассматриваемых прямых ординаты равны, поэтому 3х – 1 = - 3х + 1;
6х = 2; х = 1/3.
Ординату точки пересечения можно найти, подставив найденное значение х в любое уравнение:
У = 0
Ответ: координаты точки пересечения ( 1/3; 0 )
Задание для самостоятельного решения:
Установите, не строя графики, параллельны или пересекаются прямые у = 2х – 1 и у = 3х – 1. Если прямые пересекаются, то найдите координаты точки пересечения.