Повторение.
Прямоугольная система координат.
Линейная функция
Линейной функцией
называется функция вида ![]() ,
где k
и b
– числа
,
где k
и b
– числа
Выражение kx+b имеет смысл при любом действительном значении переменной х, т.е. область определения линейной функции – множество действительных чисел R.
Графиком линейной функции у = kx + b (k ≠ 0) является прямая, проходящая через точку (0; b) и параллельная прямой у = kx.
Так как прямая определяется двумя ее точками, то для построения графика функции y = kx+b достаточно построить две точки этого графика и через них провести прямую
Прямая, не параллельная оси Оу, является графиком линейной функции
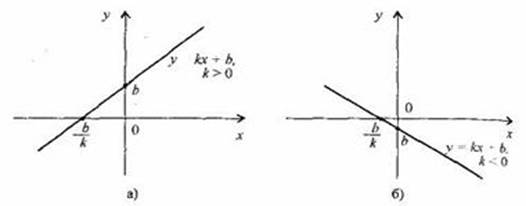
Если
b
¹
0, особый интерес представляют точки
пересечения графика линейной функции с осями координат. С осью ординат график
пересекается в точке (0,
b).
С осью абсцисс график пересекается в точке ![]() .
.
Свойства линейной функции
1. При k > 0 функция у = kx + b возрастает на области определения
2. При k < 0 функция у = kx + b убывает на области определения
3. Множеством значений функции y = kx + b (k ≠ 0) является вся числовая прямая, т.е. множество действительных чисел R
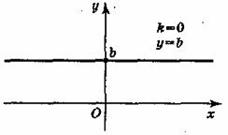
4. При k = 0 множество значений функции у = kx + b состоит из одного числа b

5. При b = 0 и k = 0 функция не является ни четной, ни нечетной
6. При k = 0 линейная функция имеет вид у = b и при b ≠ 0 она является четной
7. При k = 0 и b = 0 линейная функция имеет вид у = 0 и является одновременно четной и нечетной
Графиком линейной функции у = b является прямая, проходящая через точку (0; b) и параллельная оси Ох. Заметим, что при b = 0 график функции у = b совпадает с осью Ох
При
k
> 0 имеем, что у
> 0, если ![]() и
у < 0, если
и
у < 0, если ![]() .
.
При
k
< 0 имеем, что у > 0,
если ![]() и
у < 0, если
и
у < 0, если ![]() .
.
Графики линейных функций и их построение.