На главную / Математика / Геом

Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой ,

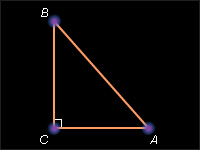
две другие стороны – катетами .

Теорема

Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Пусть Δ ABC и Δ A ₁ B ₁ C ₁ – данные треугольники и AB = A ₁ B ₁ ; AC = A ₁ C ₁ ;

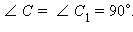Построим треугольник CBD , равный треугольнику CBA , и треугольник 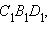равный треугольнику 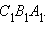Треугольники ABD и 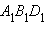равны по теореме 4.7 (третий признак). Отсюда 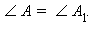С учетом условия и по первому признаку (теорема 4.1) треугольники Δ ABC и 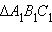равны.

Теорема доказана.

Теорема

Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один.

Пусть a – данная прямая и A – не лежащая на ней точка. Проведем через какую-либо точку прямой a перпендикулярную к ней прямую a ₁ (см. теорему 2.1), а также через точку A прямую b , параллельную прямой a ₁ (см. теорему 3.3). Она будет перпендикулярна к прямой a по следствию 4.1. Если B – точка пересечения прямых a и b , то отрезок AB – перпендикуляр, проведенный из точки A к прямой a .

Допустим, что существует другой перпендикуляр AC . Тогда у треугольника ABC будет два прямых угла, но это невозможно, так как сумма всех углов треугольника равна 180°. Теорема доказана.

Прямоугольный треугольник