В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
Каковы бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей.
Пусть A , B , C – три данные точки. Если две точки из трех или все три совпадают, то утверждение теоремы очевидно. Если все три точки различны, но лежат на одной прямой, одна из них лежит между двумя другими без ограничения общности, например, B . Тогда AB + BC = AC . Отсюда AB < AC < AC + BC , BC < AC < AC + BC , AC = AB + BC и утверждение теоремы верно.
Пусть точки A , B и C не лежат на одной прямой. Докажем, что AB < AC + BC . Опустим перпендикуляр CD на прямую AB. Точки A , B , D лежат на данной прямой и по доказанному AB ≤ AD + BD . Но AD < AC и BD < BC по построению и свойству наклонной. Отсюда AB < AC + BC . Теорема доказана.
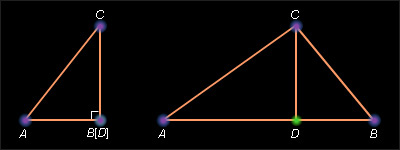
В любом треугольнике каждая сторона меньше суммы двух других сторон.
В треугольнике против большей стороны лежит больший угол.