Квадратичная функция
Квадратичной функцией называется функция, которую можно записать формулой вида
y = ax2 + bx + c,
где x – независимая переменная, a, b и c – некоторые числа, причем a ≠ 0
Рассмотрим случай, когда a = 1, b = 0 и c = 0. Формула примет вид y = x².
Вы, наверно, уже знаете, какая зависимость между площадью квадрата и длиной его стороны. Зависимость между площадью квадрата и длиной его стороны следующая: площадь квадрата равна квадрату его стороны.
А как изменяется площадь в зависимости от изменения длины стороны? Эта зависимость является примером новой функции. Чтобы поближе с ней познакомиться, построим график этой функции. Для того, чтобы построить график этой функции, нам необходимо составить таблицу соответственных значений x и y. Построим эти точки на координатной плоскости. А затем через эти точки проведём плавную линию.
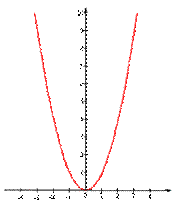
Функция y = x2
Область определения этой функции - множество R действительных чисел
Придавая переменной х несколько значений из области определения функции и вычисляя соответствующие значения у по формуле y = x2 , изображаем график функции
График функции y = x2 называется параболой
Свойства функции у = х2
1. Если х = 0, то у = 0, т.е. парабола имеет с осями координат общую точку (0; 0) - начало координат
2. Если х ≠ 0, то у > 0, т.е. все точки параболы, кроме начала координат, лежат над осью абсцисс
3. Множеством значений функции у = х2 является промежуток [0; + ∞)
4. Противоположным значениям х соответствует одно и тоже значение у, т.е. если значения аргумента отличаются только знаком, то значения функции равны, график симметричен относительно оси ординат (функция у = х2 - четная).
5. На промежутке [0; + ∞) функция у = х2 возрастает
6. На промежутке (-∞; 0] функция у = х2 убывает
7. Наименьшее значение функция принимает в точке х = 0, оно равно 0. Наибольшего значения не существует
Некоторые свойства парабол:
1. Любая прямая, параллельная оси симметрии параболы, после отражения от параболы проходит через ее фокус.
2. Касательная в любой точке параболы делит пополам угол между прямой, соединяющей точку касания с фокусом, и перпендикуляром, опущенным из этой точки на директрису.
Эти свойства парабол используют при конструировании солнечных печей, телескопов, параболических антенн.
Параболические антенны можно увидеть около любого аэродрома – они используются для того, чтобы собрать в одну точку все сигналы радиолокатора, отраженные от самолета. В прожекторах, наоборот, свет, исходящий из фокуса параболического зеркала, после отражения образует параллельный пучок и не рассеивается. По этой причине форму параболоида вращения имеют и автомобильные фары.
Свойства функции вида y = ax2 + bx + c,
где
x
– независимая переменная, a,
b
и c
– некоторые числа, причем a≠0
и вид ее графика определяются, в основном, значениями
коэффициента a
и дискриминанта 
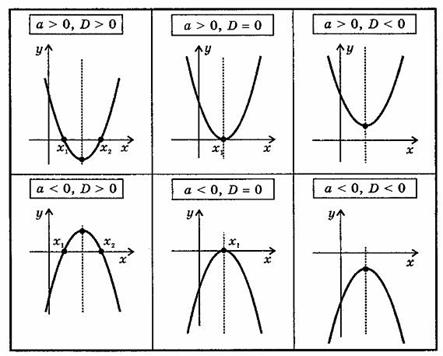
Свойства квадратичной функции
1) Область определения: R
2) Область значений при а > 0 [-D/(4a); ∞)
при а < 0 (-∞; -D/(4a)]
3) Четность, нечетность
при b = 0 функция четная
при b ≠ 0 функция не является ни четной, ни нечетной
4) Нули функции
при D
> 0 два нуля: 
,
при D
= 0 один нуль функции: 
при D < 0 нулей функции нет
5) Промежутки знакопостоянства
если, а > 0,
D > 0,
то
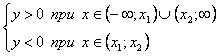
если, а > 0,
D = 0,
то 
eсли а
> 0, D
< 0, то 
если а < 0,
D > 0,
то 
если а < 0,
D = 0,
то 
если а < 0,
D < 0,
то 
6) Промежутки монотонности
при а > 0
при а < 0
Графиком
квадратичной функции является парабола –
кривая, симметричная относительно прямой 
,
проходящей через вершину параболы (вершиной параболы называется точка
пересечения параболы с осью симметрии).
Чтобы построить график квадратичной функции, нужно
1) найти координаты вершины параболы и отметить ее в координатной плоскости
2) построить еще несколько точек, принадлежащих параболе
3) соединить отмеченные точки плавной линией.
Координаты вершины параболы определяются по формулам:
;
.
