На главную /  Математика / Алгебра 9 класс / Содержание

Для тех кому интересно.

Уже древние вавилоняне для облегчения своих вычислений составляли таблицы обратных значений чисел, таблицы квадратов и кубов чисел и даже таблицы для суммы квадратов чисел и их кубов.

Математики Древней Греции старались не выражать величин числами (они знали, что существуют несоизмеримые отрезки, а понятия иррационального числа у них не было. Но все же многие их исследования оказались весьма полезными, когда через два тысячелетия стало формироваться общее понятие функции.

Долгое время понятие функции применялось не имея определенного названия. Из-за этого одни и те же рассуждения повторялись заново, и каждый ученый представлял их по-своему. Возникла необходимость введения нового термина, который позволил бы уточнить понятие и отсечь все случайное и несущественное.

Термин "функция" появился в одной из рукописей Готфрида Вильгельма Лейбница в 1673 году. Однако, он употреблял этот термин в очень узком смысле. Речь шла об отрезках касательных к кривым, об их проекциях на оси координат и о "другого рода линиях, выполняющих для данной фигуры некоторую функцию".

В 1718 году Иоганн Бернулли впервые дает определение функции, свободное от геометрических представлений: "функцией переменной называется количество, образованное каким угодно способом из этой величины постоянных". Под "каким угодно способом" во времена Бернулли понимали арифметические операции, операции извлечения корней, тригонометрические и обратные тригонометрические, показательные и логарифмические "операции", а также их различные комбинации. Такие функции теперь называют элементарными.

Леонард Эйлер в своем учебнике "Введение в анализ бесконечно малых" (1748), по которому учились целые поколения математиков, воспроизводит определение Бернулли, несколько его уточняя: "Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого переменного количества и из чисел или постоянных количеств". Как видно, в этом определении функция попросту отождествляется с тем аналитическим выражением, которым она задается.

Наряду с "явными" функциями, Эйлер рассматривал и "неявные", определяемые неразрешенными уравнениями. В то же время — в связи с знаменитой задачей о колебании струны - Эйлер считал возможным допустить в анализ не только "смешанные" функции, которые в различных частях промежутка задаются различными аналитическими выражениями, но даже функции, определяемые произвольно начерченными графиками. В предисловии к его "Дифференциальному исчислению" (1755) существует еще более общая, хотя и менее определенная формулировка: "Когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называют функциями вторых".

В течение ряда десятилетий существенного прогресса в определении понятия функции не было. Обычно приписывают Дирихле заслугу выдвижения на первый план идеи соответствия, которая единственно и лежит в основе этого понятия. В 1837 году он дал такое определение функции y от переменной x (в предложении, что x принимает все значения в некотором промежутке): "Если каждому x отвечает единственное конечное y..., то y называется ... функцией от x для этого промежутка. при этом вовсе нет необходимости, чтобы y во всем этом промежутке зависело от x по одному и тому же закону, и даже не обязательно представлять себе зависимость, выражаемую с помощью математических операций". Это определение сыграло важную роль в истории математического анализа.

Долгое время оставалось незамеченным, что Н.И. Лобачевский высказал эту идею не только раньше, но и в безупречной форме. Примыкая поначалу к точке зрения Эйлера, Лобачевский постепенно отходит от нее и в своей работе "Об исчезании тригонометрических строк" (1834) уже определенно говорит: "Общее понятие требует, чтобы функцией от x называть число, которое дается для каждого x и вместе с x постепенно изменяется. Значение функции может быть дано или аналитически выражено условием, которое подает средство испытать все числа и выбрать одно из них. Или, наконец, зависимость может существовать и оставаться неизвестной".

Привычное для нас обозначение функции — f(x) — принадлежит Эйлеру.

 

Первый способ задания функции: табличный

Если множество $ A=\mathcal{D}(f)$конечно и состоит из $ N$элементов $ x_1,x_2,\dots,x_N$, то функцию можно задать перечислением, указав, какие значения она принимает на каждом элементе $ x\in A$. Часто это делают в виде таблицы:

$ x$

$ x_1$

$ x_2$

$ \dots$

$ x_N$

$ y$

$ y_1$

$ y_2$

$ \dots$

$ y_N$

В верхней строке таблицы перечисляются все $ N$элементов конечного множества $ A$, а в нижней -- соответствующие им значения функции. Разумеется, таблицу можно расположить и в два столбца вместо двух строк.

        Пример 1.   В отделе кадров составляют таблицу, в которой в первом столбце содержатся фамилии и инициалы работников, а во втором - серии и номера их паспортов. Такая таблица задаёт функцию $ f$ -- соответствие между множеством $ A$работников предприятия и множеством $ B$кодов (код -- это серия и номер) паспортов. Полученная таблица может выглядеть, например, так:

Фамилия И.О.

Паспорт: серия,

номер

Абрамов В.П.

II-СИ

356531

Бархударов Ш.Х.

VII-ПЮ

785305

Виноградов А.В.

XII-ЧФ

015628

Гусева Т.И.

IV-БШ

764285

...

...

 


 Другая форма таблицы удобна для функции $ f:A\to B$, заданной на прямом произведении двух множеств $ A_1$и $ A_2$, то есть когда $ A=\mathcal{D}(f)=A_1\times A_2$, причём множества $ A_1$и $ A_2$конечные: $ A_1=\{x_1^{(1)},x_1^{(2)},\dots,x_1^{(m)}\}$и $ A_2=\{x_2^{(1)},x_2^{(2)},\dots,x_2^{(n)}\}$. Перечислим все элементы множества $ A_1$по вертикали, а $ A_2$ -- по горизонтали. В пересечениях строки и столбца, содержащих элементы $ x_1^{(i)}\in A_1$и $ x_2^{(j)}\in A_2$, укажем значение функции $ y_{ij}=f(x_{ij})$, где $ x_{ij}=(x_1^{(i)};x_2^{(j)})\in A_1\times A_2$:

$ A_1\diagdown A_2$

$ x_2^{(1)}$

$ x_2^{(2)}$

$ \dots$

$ x_2^{(n)}$

$ x_1^{(1)}$

$ y_{11}$

$ y_{12}$

$ \dots$

$ y_{1n}$

$ x_1^{(2)}$

$ y_{21}$

$ y_{22}$

$ \dots$

$ y_{2n}$

$ \dots$

$ \dots$

$ \dots$

$ \dots$

$ \dots$

$ x_1^{(m)}$

$ y_{m1}$

$ y_{m2}$

$ \dots$

$ y_{mn}$


Как мы видим, задание такой функции эквивалентно заданию прямоугольной таблицы -- матрицы размера $ m\times n$, элементами которой являются элементы множества $ B$.

        Пример 2.   В теории игр (одной из областей математики) рассматривается, в частности, такая задача. При взаимодействии двух партнёров $ P_1$и $ P_2$каждый из них может получить выигрыш, зависящий от вариантов действий каждого партнёра. Пусть множества вариантов действий (эти варианты называются стратегиями) партнёров конечны: $ P_1$может выбирать одну из стратегий из множества $ {\mathrm A}=\{{\alpha}_1,\dots,{\alpha}_m\}$, а $ P_2$ -- из множества $ {\mathrm B}=\{{\beta}_1,\dots,{\beta}_n\}$. Если $ P_1$выбрал стратегию $ {\alpha}_i\; (i=1,...,m)$, а $ P_2$ -- стратегию $ {\beta}_j\; (j=1,...,n)$, то однозначно определены выигрыши: у первого партнёра он равен числу $ u_{ij}=f_1({\alpha}_i,{\beta}_j)$, а у второго -- числу $ v_{ij}=f_2({\alpha}_i,{\beta}_j)$. Рассмотрим функцию $ f: {\mathrm A}\times{\mathrm B}\to\mathbb{R}^2$, такую что

$\displaystyle f:({\alpha}_i,{\beta}_j)\mapsto(f_1({\alpha}_i,{\beta}_j),f_2({\alpha}_i,{\beta}_j))=(u_{ij},v_{ij}).$

Эта функция называется функцией выигрышей или платёжным отображением игры. Её можно полностью задать, сведя все данные в таблицу вида

$ {\mathrm A}\diagdown {\mathrm B}$

$ {\beta}_1$

$ {\beta}_2$

$ \dots$

$ {\beta}_n$

$ {\alpha}_1$

$ (u_{11},v_{11})$

$ (u_{12},v_{12})$

$ \dots$

$ (u_{1n},v_{1n})$

$ {\alpha}_2$

$ (u_{21},v_{21})$

$ (u_{22},v_{22})$

$ \dots$

$ (u_{2n},v_{2n})$

$ \dots$

$ \dots$

$ \dots$

$ \dots$

$ \dots$

$ {\alpha}_m$

$ (u_{m1},v_{m1})$

$ (u_{m2},v_{m2})$

$ \dots$

$ (u_{mn},v_{mn})$


то есть задав одну матрицу, элементы которой -- пары чисел $ (u_{ij},v_{ij})$, или же задав две числовые матрицы $ f_1$и $ f_2$размера $ m\times n$:

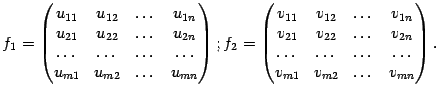
$\displaystyle f_1=\begin{pmatrix} u_{11}&u_{12}&\dots&u_{1n}\\ u_{21}&u_{22}... ...\\ \dots &\dots &\dots&\dots\\ v_{m1}&v_{m2}&\dots&v_{mn} \end{pmatrix}. $

    

 

Задачи прошедших веков, связанные с понятием функции

Пушки и учёные

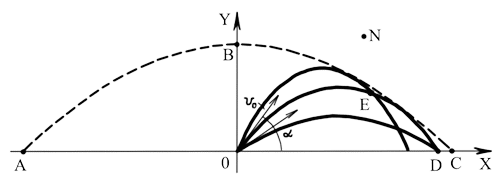
Траекторией снарядов интересовались многие ученые. Особенный интерес возник с момента изобретения пороха (в XIII веке). Ни одна тогдашняя крепость не могла долго выдержать артиллерийский огнь. Сначала применяли лишь настильный огонь, а это не давало возможности располагать артиллеристов в укреплении за холмом. Лишь позже догадались применять навесный огонь, позволяющий стрелять из-за укрытия. Чтобы обеспечить прицельность навесного огня, нужно было изучить движение тела, брошенного под углом к горизонту. Учёные доказали, что тело движется по параболе. Если при заданной начальной скорости снаряда V менять угол α, то получится бесконечное множество парабол.
Все параболы, для которых 45° ≤ α ≤ 90°, касаются одной и той же линии, имеющей уравнение

Y=½(V²/g – gx²/ V²)

Её называют параболой безопасности. Если точка N находится вне ограниченной ею области, то при начальной скорости V снаряд не попадёт в N ни при каком угле наклона.

http://graphfunk.narod.ru/images/pushki.gif

Оптические свойства параболических зеркал

По дошедшей до нас легенде Архимед построил вогнутые зеркала и с их помощью сжег римские корабли. Большинство ученых отвергают эту легенду, поскольку такие зеркала должны были бы иметь слишком большие размеры, а это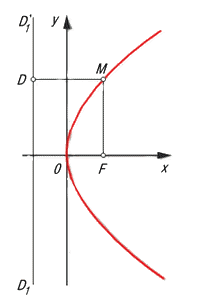parabol1 невозможно при тогдашнем уровне техники.
Но если даже история о сожжении кораблей легендарна, то все-таки сжечь римский флот при помощи параболических зеркал возможно.
Результаты, полученные Архимедом, были основаны на следующем утверждении: любая прямая, параллельная оси симметрии параболы, после отражения от параболы проходит через ее фокус. Это же свойство параболы можно сформулировать и так: касательная к любой точке параболы делит пополам угол между прямой, соединяющей точку касания с фокусом, и перпендикуляром, опущенным из этой точки на директрису.
Для того чтобы построить зеркало, собирающее солнечные лучи в одной точке, нужно отшлифовать его по параболоиду вращения – поверхности, получаемой при вращении параболы вокруг ее оси. Если направить такое параболическое зеркало на Солнце, то все отраженные лучи пройдут через фокус параболы, и температура в нем окажется настолько большой, что с помощью солнечных лучей можно будет вскипятить воду, расплавить свинец и т.д. Отсюда происходит и само название «фокус», означающее по-латыни «очаг».

 

 

 
Hosted by uCoz